Edwin V. Gray



Edwin V. Gray

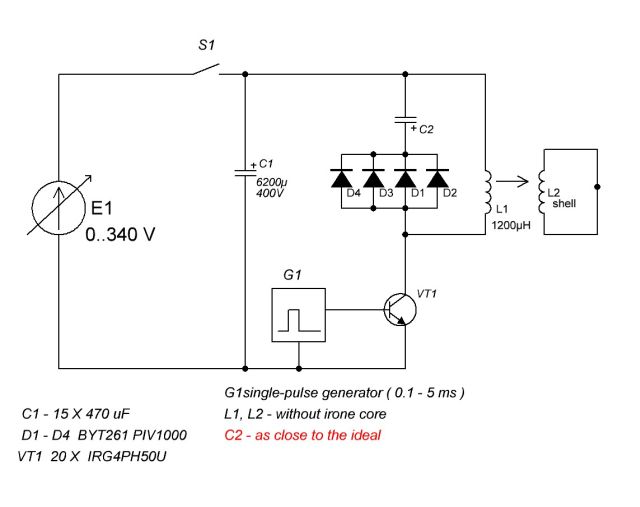
Edward V. GRAY Electro-Magnetic Association (EMA) Motor //(Pulsed Capacitance Discharge Engine)

Richard Hackenberger - Energy Management Systems

Earl M. Phinney - Pulse generating Apparatus

gray_timeline.odt

Coils in Series: Voltage: Resistance: Current: Inductance:
One Coil: 29 Volt 34 Ohm 0.9 Ampere 23.5 milliHenry
Two Coils: 29 Volt 67 Ohm 0.5 Ampere 73.7 milliHenry
Three Coils: 29 Volt 100 ohm 0.35 Ampere 118.7 milliHenry


The power source was the Voltcraft Laboratory Power Supply PS-302A with built-in voltage and current meter.

Resistance was measured with Sinometer M-830B

Inductance was measured with Voltcraft LCR-9063.

A ferrite magnet 10 mm in diameter and 4 mm thick was placed at the end of the electromagnet.

29 volts and a maximum of 0.9 amps were connected to the electromagnet and the ferrite magnet was fired many times. It reached different distances each time. But in principle, it reached the same distance regardless of the number of coils in series. An observation made was that the ferrite magnet reached longer distances when a spark occurred due to the high current at the connection and shorter distances when a spark did not occur at the connection.



Capacitor: Voltage: Stored Charge: Stored Energy:
10,000 uF: 10 Volt 0.1 Coulombs 0.5 Joules
4,700 uF: 20 volt 0.094 Coulombs 0.94 Joules
2,200 uF: 20 Volt 0.044 Coulombs 0.44 Joules


Capacitor Energy Calculator


The capacitors were fired through an MR 854 (400 volts 3 amperes) diode. How far the ferrite magnet came from the electromagnet was checked several times. Notably, 4,700 microfarads discharged at 20 volts fired the ferrite magnet longer than 10,000 microfarads discharged at 10 volts, even though the capacitor charge was identical. But the amount of energy was double by 4,700 microfarads, compared to 10,000 microfarads. Most notably, however, 2,200 microfarads discharged at 20 volts fired the ferrite magnet longer than 10,000 microfarads discharged at 10 volts, even though the capacitor charge was half for 2,200 microfarads than for 10,000 microfarads. But the amount of energy was the same.

I also found that there was a difference between discharging from a power supply and discharging from capacitors. When I discharged capacitors through a diode, it mattered more how much resistance and inductance the coils had, than when the discharge through a power supply that could deliver constant voltage and constant current. A capacitor discharging through a diode can never supply constant voltage and constant current.

Conclusion: It was Nikola Tesla who claimed that the discharge of a charged capacitor was comparable to the explosion of dynamite. That's probably why Edwin V. Gray wanted his motor to be powered by high voltage capacitor discharge. The higher the voltage the better. But 3000 volts DC was probably chosen because of the rated voltage of various components.

Hi everyone,

I have experimented today and made a great discovery that has to do with the Edwin V. Gray capacitor discharge motor.

Take two 4700 uF / 25 volt capacitors. Connect them in parallel so that you get 9400 uF / 25 volts and charge them with 9 volts from a 9 volt battery. Take an electromagnet whose one end attracts a permanent magnet. Connect a 3 amp diode in series with the capacitor and connect the diode and capacitor to the electromagnet. Check how far the permanent magnet fires.

Connect 2 4700 uF / 25 volt capacitors in series so that you get 2350 uF / 50 volts and charge them with two 9 volt batteries in series, so the total voltage is 18 volts. Take an electromagnet whose one end attracts a permanent magnet. Connect a 3 amp diode in series with the capacitor and connect the diode and capacitor to the electromagnet. Check how far the permanent magnet fires.

By entering the values in the following capacitor energy calculator: https://www.omnicalculator.com/physics/capacitor-energy

You get the current charge and the energy charge and can calculate how far the permanent magnet is fired. Is that in line with the theory?

You will find more information on my Edwin V. Gray page that I have made today: http://gratisenergi.se/gray.htm

- Hermes Atar Trismegistus

Hi Hermes,

I'm not seeing anything out of the ordinary here. Bear in mind that when you put two equal capacitors in parallel the total capacitance is doubled, and when you put them in series it's halved. Also note that when you apply a voltage to a coil the current rises linearly from zero if the inductance remains constant, and if the inductance varies (as it will if that coil is pulling in a permanent magnet) then the rate of rise of current becomes non-linear. Putting a diode in series will also make the current rise non-linear because the voltage drop over the diode depends on the current.

Thus the maximum pull here (and I'm assuming you've got springs on the magnet so that you can see the maximum pull even if you're not actually measuring it except by distance) will be different based on the capacitance and initial voltage, even when the energy in the capacitor remains (roughly) constant. If you went far enough to measure the mechanical energy you're getting out from that magnet movement (by making it do some work) you'll also find that the work you're getting out is less than the energy you're putting in. This isn't going to be an easy calculation, though, since the spring force is not constant. You'll need to calibrate the spring force at various positions of the magnet, maybe by using a spring-balance, so you know the mechanical force that spring produces at various magnet positions. Hopefully it will be pretty linear and so that will make the calculations a bit easier.

Meantime, given the number of people who have tried to replicate Gray's motor, and failed to find any OU, I think that Gray himself never actually succeeded, either. Just an error of measurement. Missed something he shouldn't have done.

Note that you can use LTspice (or other simulators) to simulate what's happening with your capacitor discharge through an electromagnet, and find the peak current and thus peak pull. You can thus get a plot of current versus time pretty easily without needing an oscilloscope and careful measurements.

At the moment I'm also getting emails from Henk, who remains convinced that he can use 3-phase power and a diode-bank to transform voltage higher whilst not reducing current, and can then use the HVDC he gets to drive an inverter and get more energy out than he put in. Basically he thinks VARs can be converted to real watts, since he's not considering the phase shift of voltage versus current on the AC side. He's relying on a DVM that tells him the RMS voltage and the RMS current, but doesn't measure phase. Doesn't seem to matter how many times I tell him that the phase is important in AC measurements.

Some things just aren't going to give you OU. Magnets and electromagnets driven by a relatively low rate of change of current are in that category. Low rate of change is anything slower than around a nanosecond at the sizes of kit you're using. You're thus several orders of magnitude too slow to even have a chance of seeing any deviations from expected results, and even then you'd need some very high fields (thus large voltages and current) which can only really be achieved using resonance. That's why the EMDrive uses a high-Q resonator and 2.45GHz, and even then the anomalous force produced is only of the order of millinewtons.

See http://physicsfromtheedge.blogspot.com/2021/02/horizon-engineers.html for another way to get an anomalous force. Note that this violates Conservation of Momentum, and thus also has the capability to violate Conservation of Enrergy. All the other "space drive" ideas (at least the ones that actually work) also have those capabilities. This is also something you can test for yourself fairly easily.

The big problem here is that nearly all of the "traditional" Free Energy devices didn't actually work. There's really not a lot of point in replicating them - lots of other people have tried and have failed to get a positive result, even when they've done all the right things. That doesn't mean that making energy is impossible, just that the methods they attempted didn't work, and that in order to succeed you need to do something different. The value of the lists of failed Free Energy inventions is in telling you what you shouldn't be doing if you want to succeed. One of those things is obviously connecting capacitors and coils, and discharging capacitors through them. No chance of success.

Best regards, Simon

Hi Warren

I am not sure but think the results of Hermes two experiments; one is the caps in parallel, (for double the UF capacitance but same voltage) the other with them with in series, (for double the voltage but half the UF capacitance) will show that the double-the-voltage series capacitors will fling that magnet much further, and by a factor in power much more than X2....so results of experiment is high voltage in caps "much better"

This because the voltage in a cap is a function of being SQUARED and its not "linear" (Actually its a function of the voltage-drop during discharge and the voltages are measured being squared in the formula (voltage before discharge squared minus the voltage after discharge squared) See the formula I will post at bottom of this, I have put it up alot...its not that complicated even I can understand it!

So thats why I think Hermes was saying he found out something important relating to the GRAY motor as the GRAY motor is very very high voltage motor up around 3000V maybe, and it was always recovering the flyback/backemf too. which is up in the 60K voltage region too.



You know where you can use those caps is the Ismael Aviso/Dmitiri 2000VDC cap discharge that flings up a shorted-out flat or donut shaped coil up around 35ft Look in FILES section here for the Dmitri/Ismael "repelling force" experiments in a folder there...Its not that hard to do basically parallel alot of mosfets for the switching and wind a couple coils, stand back and dont get killed by the 2000V...Ismael got it to work off a 9V battery, and two 1.5 batteries in series for 12V, then he could blast it 14 times (more than that actually) to 35 feet, 20 second recharge time between blasts, and batteries only dropped about a volt thats alot of power for very little input...Dmitri replicated it, has the circuits to copy etc.

Farad value of cap / ii2
X
(Voltage in cap before discharge SQUARED
MINUS
The voltage in cap after discharge SQUARED)
X
Number of discharge events per second
= Watts
So if 10,000uf cap, and the voltage sinks from 100 to 50v during discharge and you do it just once per second that is:
,01 / 2 = .005
100 squared =10,000
50 squared =2,500
10,000 - 2,500 =7,500
So;
.005 x 7,500 x 1 = 37.5 watts
Do it 10 times a revolution and its 370.5 watts.....
Monkey with the numbers, like doubling cap UF or doubling the voltage drop see what is important for more power released...

Kone

Hello Kone and thanks for the links and explanation. I think it is the voltage that drives the current through the electromagnet. 9 volts and 34 ohms provide 0.26 amps. While 18 volts and 34 ohms provide 0.53 amps. This means that for the same electromagnet with X number of turns, the double current causes the magnetomotive force to double.

I have redone the experiment and fired the permanent magnet straight into the air. The result was that the permanent magnet reached higher up in the air when I fired the electromagnet at 18 volts / 2350 uF than when I fired 9 volts / 9400 uF.

I think another reason why Edwin V. Gray used DC discharge capacitors was because a coil's reactance is zero at DC. While the reactance of a coil increases with frequency. But that's just a guess and I may be wrong.

Best Wishes, Hermes

Hi Hermes

The capacitors stores the same amount of energy when having same capacitance and same voltage across them. The difference is how they discharge that energy (i.e. doing work). When in series the capacitance is low which gives less capacitive reactance which again makes them discharge faster. As power (P) is the ratio of work (W) to time (t) Power the power is greater when the discharge happens fast even though the energy is the same. 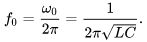Discharging a capacitor with capacitance C into an inductor with inductance L makes them oscillate at the LC resonant frequency LC Resonance The diode limits this to a half oscillation (half period). To have most power (shortest discharge time or highest frequency) requires the product of L and C to be small. Thus minimizing the capacitance requires greater tension (voltage) to store the same amount of energy. A too fast discharge may vaporize or explode the coil or demagnetize or reverse magnetize the magnet. A shorted copper ring (or disc) would do instead of the magnet as a short will reflect the magnetic field (Lenz' Law). The ring or shorted coil has to have low resistance and inductance.

Physics Demo -- Jumping Ring: https://www.youtube.com/watch?v=Pl7KyVIJ1iE (1:40). This is DC or AC and not a single capacitor discharge.

High Powered Electromagnetic Disk Launcher: https://www.youtube.com/watch?v=0BjBaRynFGQ (1:20). Outside launching.

2kV washer launcher high speed capacitor bank explosion: https://www.youtube.com/watch?v=whxiWKoj_mE (1:01). This one goes really high.

Regards
Ole

Hi folks,

I came across this page that Hermes kindly put together:

http://gratisenergi.se/gray.htm which describes a scenario about charging capacitors to different voltages and getting more energy out. I've also spent the past year or so reading everything I can about E.V. Gray and Don Smith amongst others. I'm now connecting the dots and seeing a lot of similarities between their approaches. I think it all boils down to capacitors.

Charge of a capacitor is Q = CV Energy stored in a capacitor is E = 0.5 x CV² Here is a table of some examples:

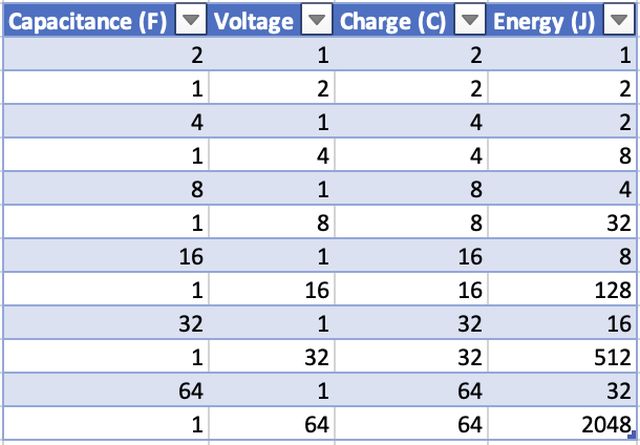
Charge-Energy

For the same charge it is very advantageous to have a lower capacitance and higher voltage as it results in much more energy.

@Hermes - did you follow this any further? It seems like something of considerable interest.

There is also the two capacitor paradox to consider. Take a 100V 100uF capacitor and connect it in series to another empty 100uF capacitor. The energy on the 100V capacitor is 0.5J. The two capacitors then equalize voltage so they have 50V each.

The energy on both capacitors is now 0.125J each, giving a total of 0.25J. Where did the extra 0.25J go? If it's possible for the energy to simply disappear, then conversely it must be possible for energy to appear.

Best regards,

Lee

Hi Lee,

I believe that the Edwin V. Gray free energy engine worked with a combination of at least three parts.

1) The lifting force of an electromagnet depends on the iron core and ampere turns. With the same iron core, the lifting force will be the same if a current of 2 amperes flows through 1 turn as if 1 ampere flows through 2 turns. My experiment with 1 and 2 and 3 coils connected in series showed that the permanent magnet landed at the same distance no matter how many coils I connected in series. The only difference was that with 1 coil the current was 0.9 ampere. With 2 coils connected in series the current was 0.5 ampere and with 3 coils connected in serie the current was 0.35 ampere.

http://gratisenergi.se/gray.htm

2) the use of pulsating high voltage DC voltage to drive enough ampere through the electromagnet which was wound with many turns and therefore had large DC resistance. Your discovery that it is better to have high voltage and small capacitor instead of low voltage and large capacitor, can be valuable. An advantage of a small capacitor compared to a large capacitor is that the small capacitor has a faster charging and the discharging time, which is suitable for working electric motors with high revolutions.

3) the use of ionizing spark gap that release electrons that increase the current through the electromagnet.

http://gratisenergi.se/sparkgap.htm

Best Wishes, Hermes

Hi Hermes,

Thanks for providing more details about your experiments with capacitors and coils.

The equations I'm looking at are:

t=RC (capacitor time constant)
Q=CV (charge)
E=(CV^2)/2 (energy)

From t=RC, we can see that a low R and low C equals a low time constant. Therefore it's much quicker to charge a small capacitance through a low resistance.

From E=(CV^2)/2, we can see that a high voltage yields much more energy due to the squaring of voltage.

Now, voltage isn't part of the time constant equation, so that means we can charge the same capacitance to varying voltages and the elapsed time will be the same.

From what I've read, it seems that voltage simply gives electrons a higher energy. In other words, voltage doesn't affect the number of electrons that are used to charge a capacitor.

My theory is that it should be possible to charge a capacitor to an extremely high voltage using a low current, and the energy produced when discharging said capacitor will exceed the input power.

It's probably a silly endeavour, but like I said earlier, I have a gut feeling about this one. I will of course publish my results regardless of how it turns out. I don't mind admitting failure.

I've performed a preliminary test where I hooked up a TV flyback transformer to a ZVS which is powered by a DC/DC converter connected to two 12V 7Ah lead acid batteries. The DC/DC converter is set to output 22V. I had a 0.01uF film capacitor inbetween the flyback positive and negative, with the negative wire not directly connected but set about 1cm away from the pin. I then had a spark gap inbetween the capacitor leads, at a distance of 2cm.

The sparks were very loud indeed and gave me quite a fright when I turned it on. The sparks looked like a white ball about 5cm in diameter. The energy in the spark looked like much more than the power being consumed by the ZVS. I recorded that the DC/DC converter was pulling 5A at 22V = 110W. I've seen sparks from a 12kV NST and they seemed feeble in comparison. Obviously empirical evidence is required, so I'm going to work on that next and record input/output.

Best regards, Lee

Hi Sven,

I've done a fair amount of research into semiconductor switches and there doesn't appear to be anything that's able to switch voltages over 3.3kV at decent amperage. For example, I'd like to dump a high voltage capacitor into a coil in a short time period, but when you calculate the instantaneous current it can amount to hundreds if not thousands of amps. I had a look at SCRs, but while they can handle the amps there is a complexity in triggering them and the rise times aren't comparable to SiC MOSFETs.

For now the humble spark gap seems to be the best and simplest approach for high voltage & high current applications. It does bring a set of new problems like electrode erosion, Ozone production etc. Maybe a vacuum tube (Thyratron) would be better and safer. Once a working voltage & amperage is arrived at then I guess it would be a good point to consider semiconductors.

Best regards,

Lee

Hi Hermes,

As I said earlier, you can use LTspice to simulate this sort of stuff. You probably need to be a little careful on the maximum timesteps, and to disable the waveform compression (.opt plotwinsize=0) so that you can see the fine details, but otherwise you're just dealing with switching capacitors around, with preferably some parasitic resistances and inductances so the components aren't too idealised.

So yep, there's an oddity that when you charge the caps in parallel, and then switch them to being in series, looks like the stored energy changes. Since this energy change happens when you simply change the wiring, and you can use switch contacts rather than semiconductors, looks like you ought to be able to produce more energy out than in pretty easily.

Bear in mind that the sum capacitance of the series caps is lower than each cap on its own. Thus if we have a set of 10 10,000µF caps which can each take 10V, and we charge them in parallel at 10V (so capacitance is 100,000µF) and then change the wiring so they are in series, you now have 100V across the set that you can drive through a resistor to measure the energy it delivers. However, the effective capacitance is now only 1000µF at 100V. You'll notice here that the capacitance is 1/100 of the parallel capacitance when in series, and the voltage is 10 times higher so the 0.5CV² comes out to being exactly the same in both configurations.

I suggest you actually set up this simulation and explore it yourself. You'll find that this doesn't allow you to produce or destroy energy, no matter how you connect them. It was just an illusion in the first place, because the whole situation wasn't considered.

Enough people have experimented in this area that, if it worked, we'd have been exploiting it for at least a century. There's nothing really special about using high voltages here - the same maths works for whatever voltage, and the sparks and arcs are actually lossy so we try to avoid them in a good design.

Of course, it's a lot cheaper and safer to do the tests using LTSpice than wiring up some real caps and putting a few kV on them. If it were a real effect, then the simulation would show the same effects since again this is mathematical in nature. As it is, the simulation shows you that there's no point in trying to produce energy this way, though it might be advantageous if you want a DC-DC converter either up or down.

Best regards, Simon



back to linkpage
suggestion
read and sign my guestbook